ETF资产配置模型分析

**资料来源：广发证券研究所
作者：马普凡

一、市场状况：配置需求为主**

　　通过研究发现ETF 的主要功能依然是实现资产配置需求。资产配置在假设所有资产长期均会跑赢货币基金的基础上，利用资产之间的低相关性实现稳定均衡的资产增值。因此，我们将研究利用国内 ETF 产品进行资产配置的可行性， 包括具体方法及收益结构的讨论。

　　资产配置是指投资者根据投资需求将资金分配在不同类别的资产类别当中，通过合理搭配不同风险-收益特性的资产来获得超额收益。与传统的单一资产模式相比，组合资产拥有减小资产风险敞口的优势。根据过去十年的市场表现来看，并不存在 一种波动稳定、持续盈利的资产(表 3)。在真实的市场中，单一资产更容易受到经济环境、宏观政策的影响。

　　其次，学术界对于资产配置的研究有深厚的积淀，对于资产标的的选择方式、各资产之间的配比以及如何进行资产的再平衡都有坚实的理论做支撑。投资者可以根据自己的需求(包括不同的投资目的，不同的风险承受能力)个性定制出适合自己的资产组合，在一定的收益水平下，将风险最小化。<p align="center">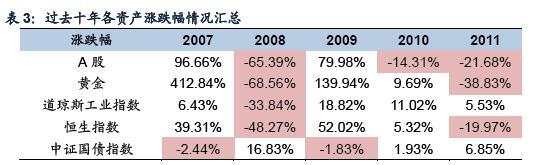</p> <p align="center">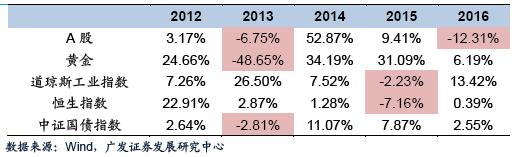</p>

　　资产配置的模型主要解决如何合理分配资产权重的问题，历史上，不同学者提出了不同的模型，可以分为固定比例资产配置模型和传统资产配置模型。

　　顾名思义，固定比例资产配置模型指的是在资产组合的配置中，各标的所占权重不变，将高风险高预期回报的主动性资产和低风险低回报的保留性资产组合到一起。比较著名的有 60/40 模型(60%股市+40%债券)、永久投资模型(25%黄金+25% 国内股票+25%现金+25%债券)等。

　　传统资产配置模型主要包括马克维茨均值-方差模型，风险平价模型，BL 模型等;改进的资产配置模型比如趋势追踪下的 TAA 资产配置模型(可以参阅报告《趋势追踪下的 TAA 资产配置模型-量化资产配置研究之二》)等。例如经典的马克维茨均值-方差模型，构建了风险和收益之间的量化平衡关系，使投资者能够按照自己的需求进行量化配置，并且实践证明是行之有效的。<p align="center">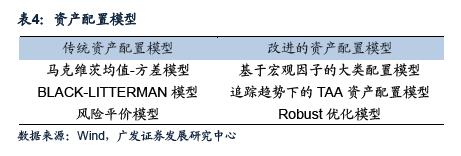</p>

二、资产类别选择：相关性低

　　资产配置第一步是对资产标的进行选择，基本原则是尽量选择不相关的资产标的(即市场表现不同的资产)，这样才能尽可能保证风险尽量分散，当某些市场表现不佳时，我们可以通过合理的调仓获得其他有利资产带来的收益。

　　本文在规模指数类ETF、行业主题指数类ETF、海外指数类ETF、货币基金型ETF、国债ETF、商品型ETF这六大类别中分别选出了成交量较多的若干ETF产品， 并对其进行相关性分析。(图19)<p align="center">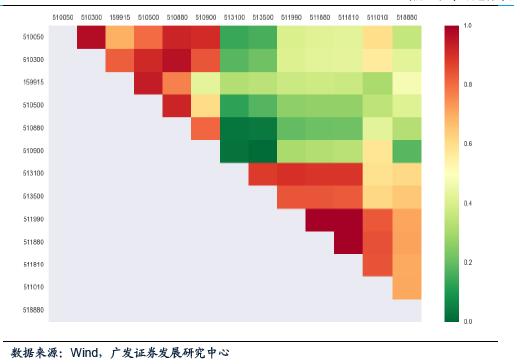</p>

　　                                                                                                 ETF相关性分析图(15)

　　上图为不同ETF产品相关性的热力图，色块的颜色标示了相关程度的高低，红 色代表相关程度高，绿色代表相关程度低。我们分别在选定的六大资产类别中各挑 选一个ETF，要求组合的相关程度最低。最终选择结果如表5所示，组合的相关性分析如图20所示，组合的风险收益分布如图21所示。由风险-收益分布图可以看出，整个资产组合不仅包含了不同类别的资产标的，也包含了不同的风险收益特性的产品。<p align="center">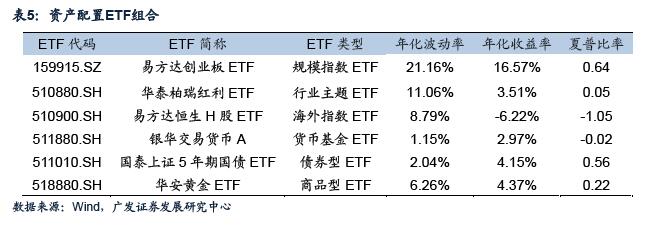</p> <p align="center">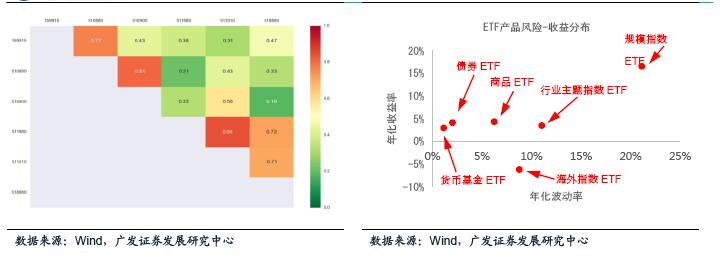</p>

三、固定权重模型：稳定性有余灵活性不足

　　我们利用历史数据对以上资产组合进行固定权重模型的测试，各固定模型的信息如表6所示。我们对以上固定比例模型进行了再平衡，回测区间是2011年1月1日到2016年12月31日。再平衡频率定为一年一次，按照ETF的买卖进行手续费的收取(最高双边各万分之三)。固定权重资产配置模型由于投资标的的多样化，有效分散了风险，但是在回测区间内获得收益并不高，并且波动率和回撤相对较为明显， 很难带来高夏普比。<p align="center">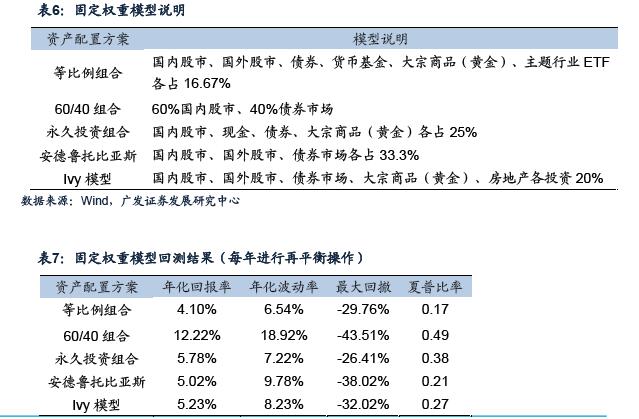</p>

四、传统资产配置模型：稳定性强，但是超额收益有限

　　对于传统资产配置模型的讨论，本文主要针对经典的马克维茨均值-方差模型和风险平价模型。在这一部分，我们首先简要介绍模型的原理，再通过实例来测试模型对ETF产品进行资产配置的效果。

　　投资者追求的是风险低且高收益的资产配置，即当在风险水平一定的时候谋求期望利益最大化，或者在一定的收益水平上尽量减少风险。马克维茨均值-方差模型就解决了风险和收益的平衡问题。

　　我们假设市场上有n种不同的金融资产，对于某一类资产 ，用 表示该资产的收益率， 表示收益率的预期， 表示 的标准差(即波动)。另外，我们假设以一年期国债收益率 作为无风险资产收益率。则资产组合P的预期收益可以表示为：<p align="center">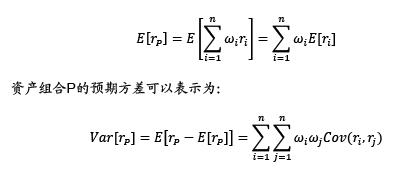</p>

　　马克维茨模型把风险和收益的平衡转化为优化问题，即在满足预期组合收益率为 的情况下，最小化风险。同时，要求满足条件：权重的和为1且不存在卖空行为。用数学语言可以表达为：<p align="center">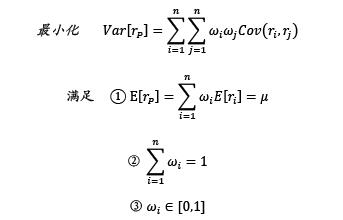</p>

　　这个问题的最优解可以通过Lagrange乘子的方法求出，当我们调节不同的 值， 我们就可以得到一组最优解，在标准差-预期收益的坐标上则表现为一条抛物线(图23)，这条抛物线被称之为“有效前沿”(只显示收益率为正的部分，并不是完整的抛物线)。图23中的每一个点都代表着一个资产组合，权重各不相同，每一个点的颜色代表了该资产组合的夏普比率(红色代表夏普比率高，蓝色代表夏普比率低)。此外，红五角形代表所有组合中最高夏普比率点，而黄色五角星代表的是最小波动率点。

　　我们可以从图中看到：1. 由于货币基金型ETF的加入，使得资产配置组合最小波动率点的风险几乎为零。2. 所有资产组合都被包裹在有效前沿抛物线以内，所以我们挑选投资组合时，尽量寻找有效前沿上的资产配置。<p align="center">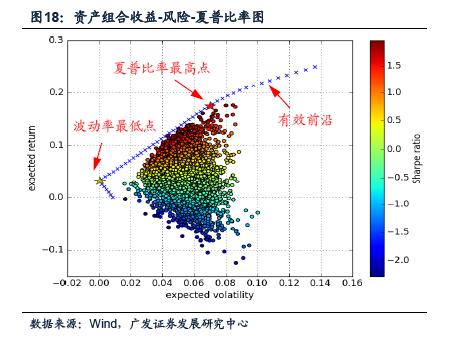</p>

　　与马克维茨模型不同的是，风险平价模型的核心思想在于给投资组合中的不同风险资产配置相应的风险权重，使得每个资产的“风险贡献”相同。例如我们假设股票的波动率为20%，而债券的波动率为5%，则我们相应的应该在组合中配置股票和债券的比例为1:4，使得这两种资产贡献的风险相同。

　　我们定义风险贡献为(其中， 为资产组合的协方差)：<p align="center"></p>

　　通过历史数据的回测，我们重点测试了马克维茨均值-方差模型(最高夏普比率以及最小波动率)和风险平价模型，回测时间区间为2011年1月1日到2016年12月31日。回测采用月度调仓的策略，手续费按照双边各万分之三收取。

　　区间内包含牛市阶段(2015年上半年)、股灾阶段(2015年下半年)以及震荡阶段(2016年上半年)。回测中，我们采用月度调仓的方式，每次调仓以过去60个交易日的数据作为依据。为了避免模型为了获得更高夏普比将大部分资金分配到货币基金ETF中影响整个资产组合的收益，我们人为限定了各个资产在组合中的权重上限和下限(表9)。据此，具体回测情况如图24和表10所示。<p align="center">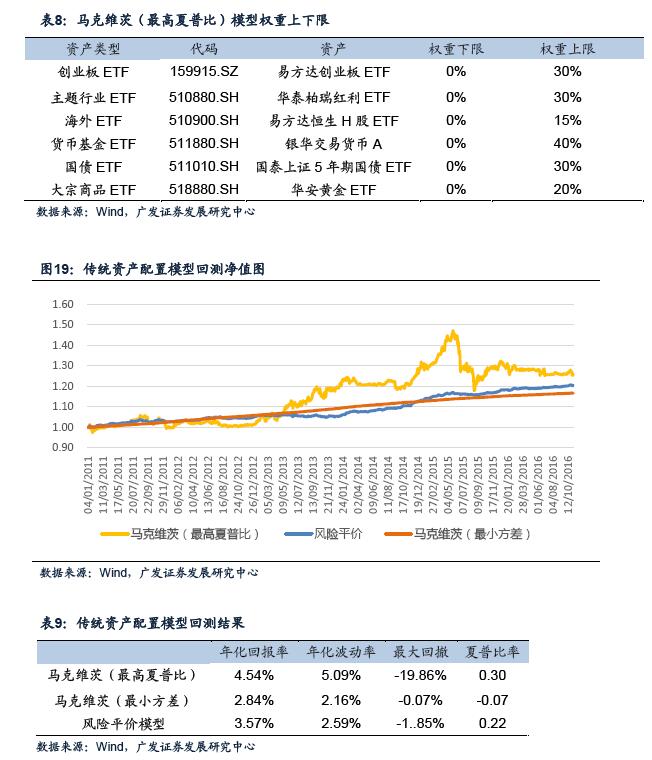</p>

　　从回测净值图中我们可以发现：

　　1. 马克维茨和风险平价模型波动较小，回撤较小，但是收益不高。这是由于资产配置组合中存在无风险资产货币基金ETF造成的，按照模型，资产中 的很大比例都被分配到购买货币基金型ETF/债券ETF，故超额收益并不高。

　　2. 只有当债券收益率(无风险收益率)下降的时候，货币基金ETF的夏普比率下降，在马克维茨模型的条件下，货币基金型ETF失去吸引力，模型才会将更多权重分配到其他资产，从而获得一定的超额收益，当然也承担相应的风险。

　　综合以上模型原理和实证表现可以看到，将传统资产配置模型应用于ETF市场稳定性较强，但是整体很难获得超额收益。原因主要有两个：1. 货币ETF占据过多份额，影响了收益;2. 月度调仓策略缺乏灵活性：若市场稳定，资产组合能够持续盈利，则没有调仓必要;若市场发生重大变化，需要及时调仓应对以减少资产组合损失。

四、改进模型：充分利用ETF流动性优势

　　针对以上传统资产配置模型的缺陷，我们对马克维茨模型进行一定改动，一方面考察其是否能够进一步提高收益，另一方面也是考察其是否能够作为机器人投资顾问产品为投资者提供一定的理财建议。具体思路如下：

　　1.将货币基金型ETF(和债券ETF)与其他ETF产品分开，当市场存在巨大风险，资产组合无法盈利的情况下，将资金转移至货币基金型ETF和债券型ETF中;如若市场存在优质资产，能够使资产组合稳定获利，则按照马克维茨模型进行权重分配。<p align="center">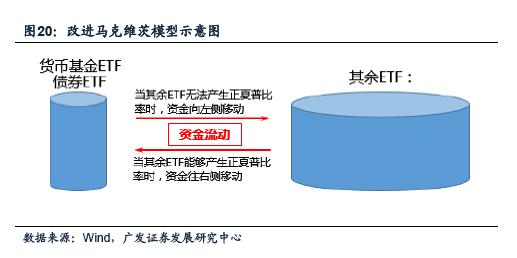</p>

　　2. 重新考量调仓策略，当最优权重发生较大改变时，进行调仓(自适应调仓)， 否则不进行任何操作，以减小操作成本(手续费)。

　　3. 由于权重优化取决于历史数据，需要对历史数据长度选择进行优化。

　　我们利用最优权重的变化来衡量是否应该调仓。即每一个交易日我们都利用历史数据和马克维茨最高夏普比率模型计算最优权重，然后通过计算当天权重与上一次调仓日最佳权重之间的欧几里得距离(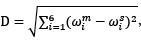，其中m代表当前日，s代表上一次调仓日)来决定是否应该调仓。当这个距离过大，则表明当前的而资产配置比例已经严重失衡，需要及时做出调整;而当距离小于指定距离阈值( )的时候，不进行任何操作。

　　利用控制变量法对距离阈值进行研究后发现，不同的距离阈值会对整个资产组合的年化收益、波动率和调仓次数产生重要影响。当我们分别采用10/30/60天历史数据作为依据进行权重计算时，总结如表11、12、13所示(回测时间区间为2011年1 月1日到2016年12月31日，手续费按照每次交易双边万分之三计算)。<p align="center">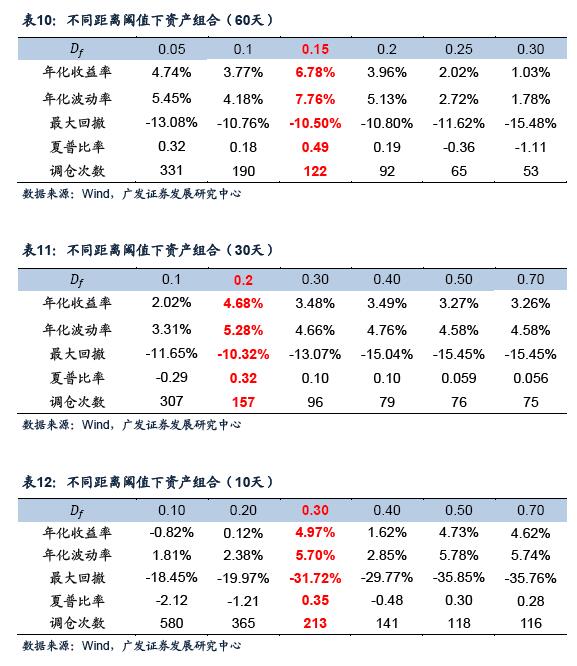</p>

　　对比以上三个表，我们能够获得如下信息：

　　1. 不同的历史回溯周期对资产组合的收益-风险均有影响。从10/30/60天的对比情况来看，较长的回溯周期对资产组合的收益是有利的。原因可能是较短的历史回溯周期容易受到市场的波动，在频繁调仓中消耗过多，无法享受到市场长期增长的福利。而长周期的回溯周期选择对于市场的短周期波动的敏感性较小，能够使收益更佳稳定。

　　2. 资产组合在不同的距离阈值下获得最高收益。距离阈值决定了资产组合的调仓的时机，对比三个不同的对照组，我们看到不同的阈值与回溯周期相匹配，即当历史回溯周期较长时，距离阈值取较小的值有利于资产组合。这是因为，当历史周期取得较长时，马克维茨模型受到市场短周期波动影响较小，最优权重的变化相应变小，所以距离阈值需要变小以应对市场的及时变化。

　　3. 距离阈值影响调仓次数，阈值越低，调仓次数增加。原因是阈值降低后， 模型的敏感性提高，市场风险稍有变化就会导致调仓。由于调仓太多直接导致成本增加，但有可能带来更佳的收益，所以实际回测结果是调仓次数与实际收益的平衡。

　　4. 通过对比改进的模型和传统模型(或固定权重模型)的回测数据，我们能够发现改进的模型在合理的参数下能够在不显著提高风险的前提下获得更高的收益。

　　从回测结果来看，用ETF产品为基础进行资产配置有很强的可操作性和控制风险获利收益能力。图26展示了以60天回溯周期(距离阈值为0.15)的条件下，资产组合的净值与创业板指数和货币基金净值的对比，我们可以发现资产组合表现虽然低于创业板指数，但是明显要更加稳定(波动率不足创业板指数的1/3)，夏普比率也要更优秀(创业板指数夏普比率：0.36;资产组合夏普比率：0.49)。与固定权重模型相比，改进后的模型表现也要稍好(60/40模型夏普比率：0.38;资产组合夏普比率：0.49)。原因是在市场出现风险时，资产组合能够通过合理调仓来避免过大的风险(减少波动)。同时与货币基金相比，又能获得风险带来的超额收益。<p align="center">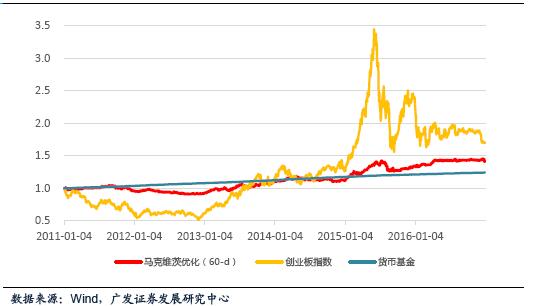</p>

　　                                                                                         资产组合净值对比图(21)

　　以ETF产品来做资产配置能够获得在一定风险控制下的合理收益，主要得益于模型的风险分散原则以及合理及时的调仓策略，在ETF较低的调仓成本下，有一定的优势。而且，这类方法完全可以依靠计算机自动实现，可以减少人为干预，从量化组合或智能投顾的角度看，不失为一种好的选择。